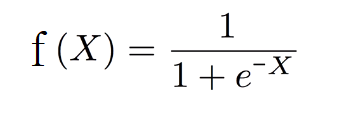여러 가지 데이터 타입 및 자료구조가 있지만, 알고리즘에 집중하기 위해 정수(int) 배열을 오름차순으로 정렬하는 형식으로 진행하겠습니다. 각각의 정렬 알고리즘은 특정 환경에 에서 최적의 성능을 발휘합니다. 메모리 공간을 적게 쓴다든지, 배열의 길이가 얼마 이하이면 제일 빠르다든지, 이미 정렬된 경우 제일 빠르다든지.... 참고로 알고리즘의 성능은 비교 횟수와 교환횟수, 추가로 사용하는 저장 공간, 초기 정렬 상태 등 에 따라 결정됩니다.
swap 함수
| /** |
| * int 배열에서 2개 원소를 서로 교환합니다. |
| * @param array 전달받은 배열 |
| * @param fromIdx |
| * @param targetIdx |
| */ |
| void swap(int[] array, int fromIdx, int targetIdx) { |
| int temp = array[targetIdx]; // 목적지 원소를 임시 저장 |
| array[targetIdx] = array[fromIdx]; |
| array[fromIdx] = temp; |
| } |
Bubble Sort(버블 정렬)
가장 단순한 정렬 알고리즘입니다. 비교하는 과정이 탄산음료를 담은 컵에 두개의 거품(크기가 서로 다른)이 수면 위로 상승하는 과정과 비슷합니다. 두 거품이 상승중에 충돌 하였을 때 큰 거품이 작은 거품보다 먼저 상승하게 됩니다.
| void bubbleSort(int[] arr){ |
| for(int i = arr.length - 1; i > 0; i --)// main loop, i 는 (배열의 길이 - 1) 에서 1까지 1씩 감소 |
| for(int j =0; j < i ; j++) // j 는 0부터 i 까지 1씩 증가하며 반복 |
| if(arr[j] > arr[j+1]) swap(arr, j, j+1); // index 가 작은 원소가 클경우 교환 |
| } |
이 알고리즘은 표준 정렬 알고리즘 중에 가장 느립니다. 이유는 데이터의 이동(교환)이 인접한 원소들 사이에서만 일어나기 때문입니다.
{7,4,3,2,1} // 초기
예를 들어 위와 같이 5개의 정수를 가진 배열이 있을때 main loop 각 1회전 할 때 7은 총 4번의 교환(swap)을 통해서 제자리를 찾아갑니다.
{4,7,3,2,1} // 내부 loop 1회전
{4,3,7,2,1} // 내부 loop 2회전
{4,3,2,7,1} // 내부 loop 3회전
{4,3,2,1,7} // 내부 loop 4회전
버블 정렬에 있어서 최선의 경우와 최악의 경우 사이의 유일한 차이는 교환 연산의 실제 수행 횟수입니다. 이미 정렬되어있는 배열인 경우 비교 연산만 일어나고, 교환 연산은 일어나지 않습니다. (최선의 경우)
time : worst O(n^2), best O(n), average O(n^2)
Selection Sort(선택정렬)
버블 정렬보다 약간 더 효율적입니다. 자료의 이동을 최소화하려는 목적으로 만들어져서 자료의 양이 적을 때 아주 좋은 성능을 발휘합니다.
| void selectionSort(int[] arr){ |
| for(int i = arr.length - 1; i > 0; i --) { |
| int maxIndex = 0 ; // 배열 원소중 max 값의 index를 저장할 변수 |
| for(int j = 1; j <= i ; j++) |
| if(arr[j] > arr[maxIndex]) maxIndex = j; |
| swap(arr, maxIndex, i); |
| } |
| } |
main loop의 각 회전마다 정렬되지 않은 원소 중에서 가장 큰 원소를 선택하여 그것을 올바른 위치로 이동시키기 때문입니다. 예를 들어 아래의 배열을 정렬합니다.
{7,4,3,2,1} // 초기
{1,4,3,2,7} // main loop 1회전 후
main loop 가 1회전 하면 7은 가장 오른쪽에 배치됩니다. 이때 교환(Swap) 연산은 1 과 7 사이에 한 번만 실행됩니다. 데이터 이동(교환) 은 선형 시간에 실행되어 버블 정렬보다 빠릅니다.
time : worst O(n^2), best O(n^2), average O(n^2)
Insertion Sort(삽입정렬)
위의 버블, 선택 정렬과 다르게 main loop의 i가 를 점점 증가합니다.
| void insertionSort(int[] arr){ |
| for(int i = 1; i < arr.length; i++) { |
| // i가 0이 아니라 1부터 시작합니다. i가 0인 loop 는 비교할 원소가 없습니다. |
| int ai = arr[i]; // 정렬된 앞 배열에 삽입될 원소, 위치를 찾을 때까지 임시저장. |
| int j; // 비교 연산 및 이동 연산을 한 임시 변수 |
| for (j = i; j > 0 && arr[j-1] > ai; j--) // 정렬된 배열에서 ai 보다 큰 값이 나올 때까지 j 감소 |
| arr[j] = arr[j - 1]; // 원소가 한 칸씩 우측으로 이동 |
| arr[j] = ai; // 마지막으로 나온 j에 ai 를 삽입 |
| } |
| } |
삽입정렬은 데이터 이동 횟수는 버블, 선택정렬에 비교해 많지만 그 정렬보다 느리진 않습니다. 그 이유는 평균적으로 삽입정렬은 비교하는 횟수가 절반으로 감소하기 때문입니다. 거의 정렬되어 있을 때 가장 빠른 알고리즘입니다.
time : worst O(n^2), best O(n), average O(n^2)
Shell Sort(셸 정렬)
셸 정렬 은 비교정렬(bubble, selection, insertion, shell) 중에서 가장 성능이 뛰어난 알고리즘입니다. 그리고 이후에 나올 퀵 정렬 다음으로 수행속도가 빠르고 안정적입니다. gap = array.length / k로 정합니다. 저는 k 를 간단히 2로 정하였는데 k에 따라 성능이 좌우됩니다.
| /** |
| * 셸 정렬에 의해 나누어진 부분 배열을 정렬할 삽입 정렬 알고리즘 |
| * @param array 배열 |
| * @param startIndex 시작 인덱스 |
| * @param gap 증분 |
| */ |
| void customInsertionSort(int[] arr, int startIndex, int gap) { |
| for(int i = startIndex + gap; i < arr.length; i+=gap) { |
| // 삽입정렬과 다르게 i가 startIndex + gap에서 시작하고 증분이 1이 아니고, gap이 된다. |
| int ai = arr[i]; |
| int j; |
| for (j = i; j > startIndex && arr[j-1] > ai; j--) // j > 0 대신 j > startIndex 사용 |
| arr[j] = arr[j - 1]; |
| while (j > gap && arr[j-gap] > ai) { // arr[j-1] 대신에 arr[j-gap] 을 사용 |
| arr[j] = arr[j-gap]; // arr[j-1] 대신에 arr[j-gap] 을 사용 |
| j -= gap; |
| } |
| arr[j] = ai; |
| } |
| } |
|
|
| // 쉘 정렬 |
| void shellSort(int[] arr){ |
| for(int gap = arr.length/2; gap > 0; gap /= 2) { // main loop, gap 을 2씩 나눔.. 4, 2, 1 |
| for (int startIndex = 0; startIndex < gap; startIndex++) |
| customInsertionSort(arr, startIndex, gap); |
| } |
| } |
셸 정렬은 기존 배열을 여러개의 sub sequence(부분 배열)로 분할하고 이에 대해서 삽입정렬 합니다. (병렬화) 이 sub sequence는 gap(증분) 을 이용해서 정의합니다. 저는 위의 코드에서는 gap 을 초기에 전체 길이의 1/2 로 잡았습니다. 전체 길이가 8인 다음 배열이 있습니다.
{a1,a2,a3,a4,a5,a6,a7,a8} // 초기 배열, 배열길이 8
위의 배열에서 처음 gap = 8/2 = 4 입니다.
{a1,a5} {a2,a6} {a3,a7} {a4,a8} // 원소를 4칸씩 건너뛰고 부분 배열을 생성. 각각 삽입정렬을 수행, 총 4회 삽입정렬
// iSort(a,0,4);
// iSort(a,1,4);
// iSort(a,2,4);
// iSort(a,3,4);
위의 4가지 sub sequence 로 나누어져서 main loop 1번째 회전이 끝날동안 이루어집니다.
이후 2회전에서는 gap = 4/2 = 2 입니다.
{a1,a3,a5,a7} {a2,a4,a6,a8} // // 원소를 2칸씩 건너뛰고 부분 배열을 생성총 2회 삽입정렬
// iSort(a,0,2);
// iSort(a,1,2);
위의 2가지 sub sequence 각각에 대하여 main loop 2번째 회전에 이루어집니다. 마지막에 전체를 대상으로 삽입정렬하여 마무리합니다. (gap = 2/2 = 1)
{a1,a2,a3,a4,a5,a6,a7,a8}
// iSort(a,0,1);
1회전 이후에 나오는 sub sequence(크기가 m) 들은 절반은 정렬된 상태이기 때문에 m/2 이상의 비교를 수행하지 않습니다.
gap 은 적당한 매개변수를 선택하여 그 값만큼 간격을 가진 데이터들을 하나의 시퀀스로 모아 삽입정렬을 실행합니다. (2가 아니어도 됩니다.) 이후에 적당히 줄여나가면서 정렬을 반복하고, 매개변수 값이 1이되면 종료합니다. 이 때, 매개변수는 근사적으로 소수여야합니다.
time : worst O(n^2), best O(n logn), average O(n^1.5) - gap 의 값에 따라서 성능이 좌우됩니다.
Merge Sort(합병정렬, 병합정렬)
분할-정복 프로세스를 사용한 알고리즘입니다. 합병 정렬은 분할하는 알고리즘과 합볍하는 알고리즘이 필요합니다. 이 2가지 배열을 합병하는 알고리즘은 3개의 큐를 생각는 것이 가장 좋습니다.
| /** |
| * 비순환 드라이버 method |
| * @param arr |
| */ |
| void mergeSort(int[] arr) { |
| mergeSort(arr,0,arr.length); |
| } |
|
|
| /** |
| * 합병 정렬 - 분할하는 로직이 들어있고, 다른 합병정렬 알고리즘을 가지고 있는 함수를 실행합니다. |
| * @param arr 배열 |
| * @param startIndex 시작 index |
| * @param last 처음에 배열의 길이를 입력 받고, -1 해서 마지막 인덱스로 사용됩니다. |
| */ |
| void mergeSort(int[] arr, int startIndex, int last) { // 오버로드로 선언 매개변수 개수만 다릅니다. |
| // 선조건 : 0 < startIndex < last <= arr.length |
| // 후조건 : arr[startIndex...last-1]은 오름차순이다. |
| if(last - startIndex < 2) return; |
| int middleIdex = (last + startIndex) / 2; // 배열의 중간 index |
|
|
| mergeSort(arr, startIndex, middleIdex); // [startIndex, middleIdex) 반열린구간 |
| mergeSort(arr, middleIdex, last); // [middleIdex, last) 반열린구간 |
| merge(arr, startIndex, middleIdex, last); |
| } |
|
|
| /** |
| * 합병하는 알고리즘입니다. |
| * @param arr |
| * @param startIndex |
| * @param middleIdex |
| * @param last |
| */ |
| void merge(int[] arr, int startIndex, int middleIdex, int last) { |
| // 선조건 : arr[startIndex...middleIdex-1] 과 arr[middleIdex...last-1] 은 오름차순이다. |
| // 후조건 : arr[startIndex...last-1] 은 오름차순이다. |
| if(arr[middleIdex -1] <= arr[middleIdex]) return; |
| int i = startIndex, j = middleIdex, k = 0; // k는 합병된 원소의 개수입니다. |
| int[] tempArr = new int[last - startIndex]; // 합병할때만 사용하는 임시 배열 |
| while (i < middleIdex && j < last) // main loop |
| if(arr[i] < arr[j]) tempArr[k++] = arr[i++]; |
| else tempArr[k++] = arr[j++]; |
| if(i < middleIdex) System.arraycopy(arr, i, arr, startIndex + k, middleIdex - i); |
| // shift arr[i...midddleIndex - 1] |
| System.arraycopy(tempArr, 0, arr, startIndex, k); // copy tempArray[0...k-1] to arr[p...p+k-1] |
| } |
위의 합병하는 로직이 있는 merge 함수에 main loop 가 종료되면 tempArr에는 두배열을 합친 정렬된 원소들이 들어있습니다. 그런데 2배열중에 좌측에 있는 배열에 합병되지 않은 원소가 생기는 경우가 있습니다.
if(i < middleIdex) System.arraycopy(arr, i, arr, startIndex + k, middleIdex - i);
이때 위처럼 좌측 끝에 합병되지 않는 원소들을 끝으로 옮겨주는(shift) 작업이 필요합니다. k는 합병 정렬된 원소의 개수입니다. k 는 tempArr.length 와 같습니다.
일반적인 분할-정복프로세스에는 log n 단계의 분할과 log n 단계의 병합이 이루어집니다. 따라서 2log n 레벨을 가집니다. 각각의 레벨에서 n개의 원소가 비교되므로, 최대 비교 횟수는 2n * log n 번입니다. 실제로는 시간이 오래 걸리며, 외부정렬(대용량의 외부 기억장치를 사용하는 정렬 - 대용량 데이터를 정렬할 수 있습니다.)에 주로 활용합니다.
time : worst O(n logn), best O(n logn), average O(n logn)
Quick Sort(퀵 정렬)
pivot(피벗)을 활용하여 분할-정복 알고리즘을 사용하였습니다. 배열에서 pivot 을 정하고, 그것을 임시 보관한뒤 이를 중심으로 pivot 보다 작은그룹, 큰그룹 으로 나누고, 그 사이에 pivot 을 위치시킵니다.
| /** |
| * 비순환 드라이버 method |
| * @param arr |
| */ |
| void quickSort(int[] arr) { |
| quickSort(arr,0,arr.length); |
| } |
| |
| /** |
| * 퀵 정렬 |
| * @param arr 배열 |
| * @param startIndex 시작 index |
| * @param last 처음에 배열의 길이를 입력 받고, -1 해서 마지막 인덱스로 사용됩니다. |
| */ |
| void quickSort(int[] arr, int startIndex, int last) { |
| if(last - startIndex < 2) return; |
| int j = partition(arr, startIndex, last); |
| quickSort(arr, startIndex, j); |
| quickSort(arr, j + 1, last); |
| } |
| |
| /** |
| * pivot 보다 큰 원소를 우측으로 작은 원소를 좌측으로 보내면서 마지막에 pivot 의 위치를 찾고 반환 |
| * @param arr |
| * @param startIndex |
| * @param last |
| * @return pivot 의 index 를 반환합니다. |
| */ |
| int partition(int[] arr, int startIndex, int last) { |
|
|
| int pivot = arr[startIndex]; // 맨 앞에 있는 원소를 pivot정한 경우입니다. |
| int i = startIndex, j = last; |
| while (i < j) { // i == j 가 되면 loop 가 종료됩니다. 회전할때 마다 i가 증가되거나 j가 감소 됩니다. |
| while (j > i && arr[--j] >= pivot) ; //empty loop, j는 pivot 이 될때까지 1을 선감소 |
| if(j > i) arr[i] = arr[j]; // arr[j]는 arr[i]로 복사되고, 빈공간이되었다고 봅니다. |
| while (i < j && arr[++i] <= pivot) ; //empty loop, i는 pivot 이 될때까지 1을 선 증가 |
| if(i < j) arr[j] = arr[i]; // arr[i]는 arr[j]로 복사되고, 빈 공간이 되었다고 봅니다. |
| } |
| arr[j] = pivot; // i == j 인 상태입니다. |
| return j; |
| } |
평균적인 경우에 quick sort는 최선의 경우에 비교해 약 38% 정도만 더 비교를 수행합니다. 또한, 최선의 경우 퀵 정렬은 합병 정렬과 마찬가지로 반복적으로 시퀀스를 2개 부분배열과 한 개의 pivot으로 나눕니다.
퀵 정렬이 합병 정렬에 비교해 빠른 가장 큰 이유는 "제자리(in place)"에서 동작하는 것입니다. 모든 데이터 이동은 분할 프로세스에 의해 만들어지는 회전 때문에 수행되는데, 여기서는 하나의 임시 저장 위치(피벗을 위한)만을 사용합니다. 합병정렬은 임시저장소로 배열 전체를 사용하며, 배열에서 배열로 복사하는 데 시간이 걸리게 됩니다.
만약 배열이 이미 오름차순으로 정렬된 경우, 맨 앞에 있는 원소를 pivot으로 정할 경우 최악의 성능을 내게 됩니다. (pivot의 위치 어디에 선언하느냐에 따라 partition method의 source code도 달라집니다.) 이를 피하고자 java.util.Arrays.sort() 는 내부적으로 수정된 퀵 정렬을 사용하고 있습니다.
time : worst O(n^2), best O(n logn), average O(n logn)
Heap Sort(히프 정렬)
히프 정렬은 선형시간이 아니라 로그 시간에 각각의 선택을 수행할 수 있도록 선택 정렬을 개선한 것으로 볼 수 있습니다. 이것은 정렬되지 않은 부분 배열을 heap으로 유지하고, 최댓값이 a[0]에 위치하도록 합니다. 여기서 각각의 선택이란 a[0]를 내보내고 나서, 나머지 정렬되지 않은 부분 배열을 다시 히프화(heapify) 하는 것입니다. 이러한 연산은 단순히 히프화 연산을 사용하면 되므로, log n의 단계가 걸리게 됩니다.
| /** |
| * heap 정렬을 합니다. |
| * @param arr |
| */ |
| void heapSort(int[] arr) { |
| for (int i = (arr.length - 1) / 2 ; i >= 0; i--) |
| heapify(arr, i, arr.length); // 모든 내부 node를 index가 큰 node 부터 root node(arr[0])까지 히프화합니다. |
| // arr[0](root node)에는 최댓값이 들어가고 모든 서브트리가 heap 이됩니다. |
| for (int j = arr.length - 1; j > 0; j--) { |
| swap(arr, 0, j); // 0번 원소와 j번 원소를 교환합니다. |
| heapify(arr, 0, j); // [0,j) 구간을 히프화 합니다. |
| } |
| } |
|
|
| /** |
| * 전달받은 node 번호와 자식 노드를 비교하여 히프화합니다. |
| * @param arr |
| * @param nodeIndex 히프화할 node 의 번호입니다. |
| * @param heapSize 완전 이진 트리의 크기입니다. |
| */ |
| void heapify(int[] arr, int nodeIndex, int heapSize) { |
| int ai = arr[nodeIndex]; |
| while (nodeIndex < heapSize/2) { // arr[i] 는 leaf 가 아닌경우만 loop 를 순환합니다. |
| int j = 2 * nodeIndex + 1; // j는 ai의 좌측 자식 노드의 index 입니다. |
| if(j + 1 < heapSize && arr[j + 1] > arr[j]) ++j; // 우측 자식 노드의 값이 더 큰 경우 j를 후증가합니다. |
| if(arr[j] <= ai) break; // 부모가 자식노드보다 크면 loop 를 종료합니다. |
| arr[nodeIndex] = arr[j]; |
| nodeIndex = j; |
| } |
| arr[nodeIndex] = ai; |
| } |
히프 정렬은 알고리즘 적으로 선택정렬과 삽입 정렬을 조합한 것으로 볼 수 있습니다. 히프정렬은 2단계로 구분할 수 있습니다. 첫 번째로 히프를 구축하고, 다음으로 제거하는 것을 통해 정렬합니다. 2단계 사이에서 히프는 부분 순서화 됩니다. 따라서 알고리즘은 삽입에 대해 부분정렬을 수행하고, 삭제에 대해 부분 정렬을 수행한다. 2개의 느린 알고리즘을 조합하여 빠른 알고리즘을 생성한 것입니다.
time : worst O(n logn), best O(n logn), average O(n logn)
Counting Sort(계수 정렬)
서로 다른 숫자 값이 키의 개수보다 훨씬 적은 경우 잘 동작하는 정렬 알고리즘입니다.
| void countingSort(int[] arr) { |
| int n = arr.length; |
|
|
| int output[] = new int[n]; // 결과를 저장할 임시 배열 |
|
|
| int count[] = new int[256]; // arr 에 정수 입력값중에 255 를 넘어가는 건 정렬되지 않습니다... |
|
|
| for (int i = 0; i < n; ++i) |
| ++count[arr[i]]; // 계수 를 측정합니다. |
|
|
| for (int i = 1; i < 256; ++i) // 앞의 원소를 더하여 누적시킵니다. |
| count[i] += count[i - 1]; |
|
|
| for (int i = n - 1; i >=0; i--) { |
| // 같은 키의 순서를 유지하기 위해 n-1에서 0으로 내려가면서 역순으로 실행하였습니다... |
| output[count[arr[i]] - 1] = arr[i]; // output 배열에 실제 정렬을 수행합니다. |
| --count[arr[i]]; // 정렬된 원소는 counting 계수를 1 감소시킵니다. |
| } |
|
|
| for (int i = 0; i < n; ++i) |
| arr[i] = output[i]; // 원본 배열에 결과를 저장 |
| } |
일반적으로 같은 키가 뒤섞이지 않도록 하는 정렬 알고리즘을 안정적(stable)이라고 합니다. 계수 정렬은 안정적인 정렬 알고리즘입니다. 계수 정렬의 중요한 응용중의 하나는 다차원 정렬(multidimensional sorting) 입니다. 기수 정렬이라고도 합니다.
Radix Sort(기수 정열)
계수 정렬의 다차원 응용에 해당하는 알고리즘입니다. 모든 key가 같은 d(문자열의 길이)를 가지는 string(문자열)이고, string에 있는 모든 문자는 정수집합{0,1... r-1}에 속해있다고 가정합니다. 예로 다음과 같은 것들이 있다.
- SSN(미국사회보장번호, 055-23-2233) : d = 9, r=10
- ISBN(도서 번호, 3-35463-943-X) : d = 1, r = 11
다음은 10자리 정수까지 정렬하는 기수정렬 예시입니다.
| void radixSort(int[] arr) { |
| int[] result = arr ; |
| for (int place = 1; place <= 1000000000; place *= 10) { |
| result = countingSort(result, place); |
| } |
| for (int i = 0; i < arr.length; i++) { |
| arr[i] = result[i]; |
| } |
| } |
|
|
| int[] countingSort(int[] input, int place) { |
| int[] out = new int[input.length]; |
|
|
| int[] count = new int[10]; |
|
|
| for (int i = 0; i < input.length; i++) { |
| int digit = getDigit(input[i], place); |
| count[digit] += 1; |
| } |
|
|
| for (int i = 1; i < count.length; i++) { |
| count[i] += count[i - 1]; |
| } |
|
|
| for (int i = input.length - 1; i >= 0; i--) { |
| int digit = getDigit(input[i], place); |
|
|
| out[count[digit] - 1] = input[i]; |
| count[digit]--; |
| } |
|
|
| return out; |
|
|
| } |
|
|
| int getDigit(int value, int digitPlace) { |
| return ((value / digitPlace) % 10); |
| } |
Buket Sort(버킷 정렬)
특정한 경우에만 효율적인 알고리즘입니다. 버킷 정렬의 실제 비용은 n개의 버킷을 할당하는 것입니다. 이러한 오버헤드는 이 알고리즘을 대부분의 경우 비실용적인 것으로 만듭니다.
| void bucketSort(int[] a, int maxVal) { |
| int [] bucket=new int[maxVal+1]; |
|
|
| for (int i=0; i<bucket.length; i++) { |
| bucket[i]=0; |
| } |
|
|
| for (int i=0; i<a.length; i++) { |
| bucket[a[i]]++; |
| } |
|
|
| int outPos=0; |
| for (int i=0; i<bucket.length; i++) { |
| for (int j=0; j<bucket[i]; j++) { |
| a[outPos++]=i; |
| } |
| } |
| } |
java.util.Arrays.sort() method
자바 유틸 클래스 중에 Arrays에 포함된 sort 함수 내부는 퀵 정렬과 합병 정렬을 이용해서 구현되었습니다. boolean을 제외한 각각의 primitive type(기본형) 배열을 위한 sort() 함수와 Object type 배열을 위한 sort() 함수를 가지고 있습니다. 기본형을 위한 sort() 함수는 개선된 quick sort 알고리즘을 사용하고, Object를 위한 sort() 함수는 개선된 합병 정렬을 사용합니다. quick sort는 순환호출이 작은 부분배열로 내려가게 되면 약간 비효율적이게 되는데, 길이가 일정한 경곗값보다 작아지게 될 때 부분배열을 정렬하는 순환 호출이 비순환 알고리즘으로 전환된다면 알고리즘은 더 빨리 지게 됩니다. 이를 위해 sort() 함수는 내부적으로 경곗값을 7로 설정하였고, 부분배열의 길이가 7보다 작아지게 되면 삽입정렬을 호출하게 되어있습니다. 여기에 더해서 pivot을 선택할때, 첫 번째, 마지막, 가운데 원소 중에서 중간값을 선택하도록 하였습니다. 이렇게 하여, 이미 정렬되어있는 배열에 대해서 최악의 경우 O(n^2)가 발생하는 것을 방지해줍니다.
Object를 위한 개선된 합병정렬은 기본형과 마찬가지로 배열의 길이가 경곗값 7 보다 작아지면 삽입정렬로 전환됩니다. 또한, 여기에 불필요한 합병을 피하는 방법을 구현하였습니다. 합병에 대한 호출은 첫 번째 배열의 마지막 원소가 두 번째 배열의 첫 번째 원소보다 큰지를 검사합니다. 만일 크지 않다면 선형 시간을 가지는 합병 정렬대신 간단한 상수 시간을 가지는 연결(concatenation)을 수행합니다.